高校時代の数学の話になるので、もう忘れてしまっている人も多いでしょうし、逆に理系の人には当たり前すぎる知識でもありますが、三角関数のうちsin0°、sin180°、cos90°、cos270°は0になります。
技術系のお仕事をされている方であれば知っている人も多いかもしれませんが、三角関数をエクセルで計算しようとすると、ここにちょっとしたトラップがあります。
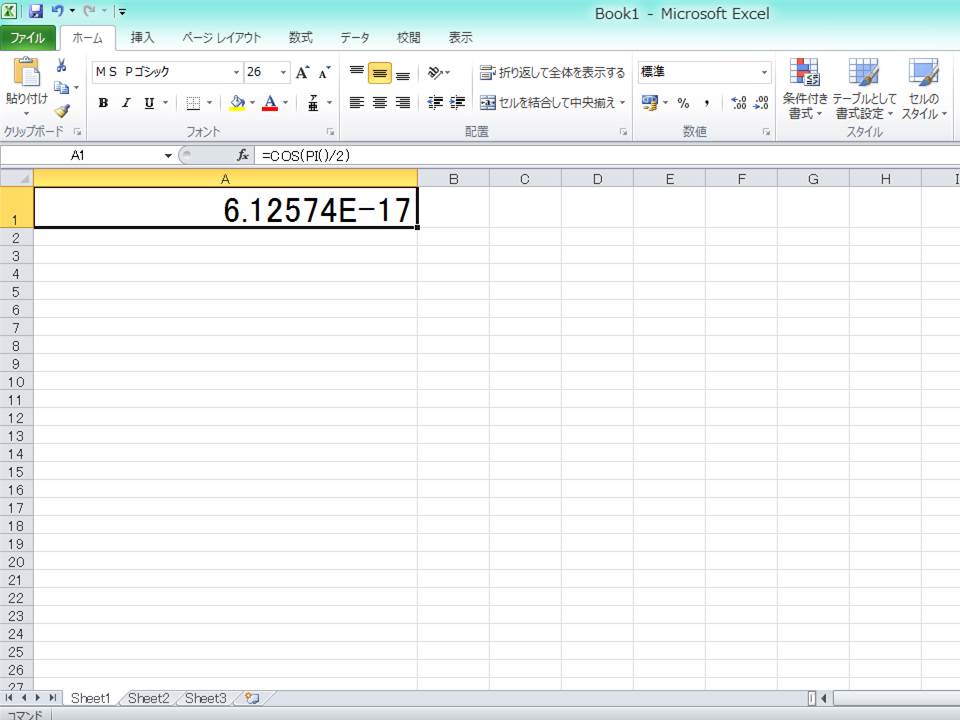
cos90°をエクセルで入力すると、0にならず、6.12574E-17という、限りなく0に近い小さい数字が出てきてしまいます。
え、0じゃないの?
初めてこの場面に遭遇すると、エクセルぶっ壊れた?なんて思われる方も多いかもしれませんが、よくよく考えてみると、こうなるのも自然なことです。
〇三角関数はラジアンで計算
エクセルで三角関数を計算するときは、度数ではなくてラジアンで計算することになります。45°であればπ/4、90°であればπ/2。エクセルで入力する時は、COS(PI()/2)とかSIN(PI()/6)という具合に入力します。
πは皆さんご存知の円周率で、どこまでも続く割り切れない数字です。そう、あのどの桁まで覚えられるかを競う、あの円周率です。
π=141592653589793238462643383279502884197169399375105820974944・・・
これでもまだまだ終わらないのが円周率です(´ε`;)しかし、エクセルのπは、どこかで四捨五入された数字になるので、ラジアンで計算すると、きっちり0にならないわけです。
エクセルで出力されるcos90°の値は、90°ではなく、89.9999°とか、90.00001°のように、90°に限りなく近い数字になります。
別にエクセルがぶっ壊れているわけではなく、割り切れない数字を扱っているので当たり前なのです。もちろんsin180°を計算しても、ちょうど0にはならず、限りなく0に近い、0ではない数字が出てきてしまいます。
何らかのデータを算出する時は、ほとんど気にならない違いかもしれませんが、P×L×cosθみたいな計算をする場合、cos90°=0のはずなのに、計算結果が0にならない。なんじゃこりゃ?ってことになってしまうので、こういう時は、手動で0を入力することになります。
ちょっと面倒ですが、これがエクセルの限界になります。オイラーの公式eiθ=cosθ+isinθで、θ=πの時はeiπ=-1になりますが(一部で美しい公式と言われているらしい)、これもエクセルで計算しようとすると、-1にはならず、-1に限りなく近い数字が出てきます。
そんなに気にするような話ではないと思うので、そんなに役に立つ話かどうか微妙ですが、頭の片隅に入れておいて損はない話です。
ただ、エクセルでこのような計算をする機会の多い人にとっては、エクセル関数の一覧表を見るほうが大事なのは間違いないですが……(・・;)